
DPP Education
Welcome to DPP, where your coding journey takes a daily step forward!
Whether you're just starting to learn coding or you're a seasoned developer looking to stay sharp, we’ve got something for everyone. Each day, we deliver a hand-picked coding challenge straight to your inbox—designed to help you grow, improve, and tackle new problems with confidence.
Why Daily Practice Problems?
Consistency is key when it comes to mastering any skill. Coding is no different. With a daily challenge, you create a habit of problem-solving, building new concepts, and applying them to real-world scenarios. Our questions are carefully crafted to cover a wide range of difficulty levels and programming languages, ensuring that you’re constantly learning and improving, no matter where you are in your coding journey.
What Makes Us Different?
- Tailored for All Skill Levels: Whether you're a beginner learning the basics or an experienced developer tackling advanced algorithms, our questions are categorized by difficulty, so you’ll always be working at your level. Plus, we mix it up, so you’ll never get bored!
- Diverse Topics: We cover a wide variety of topics—from data structures and algorithms to web development, databases, and even machine learning. Our challenges are designed to provide a well-rounded experience, helping you become a versatile coder.
- Learn at Your Own Pace: No pressure, no deadlines—just a daily prompt that you can solve whenever it fits your schedule. You can even take your time on more challenging questions and come back to them when you’re ready.
- Boost Your Confidence: Coding is all about practice and persistence. By tackling a new problem every day, you’ll build not only your knowledge but your problem-solving confidence. You’ll start approaching coding challenges with a fresh mindset, ready to take on even the toughest problems.
Ready to Start?
It's simple to begin! Just sign up with your email, and we’ll send your first coding question directly to your inbox. No ads, no spam—just daily challenges to help you grow as a coder. Every day brings a new opportunity to improve, and with our expert-curated questions, you'll stay motivated, engaged, and excited about coding.
You are given a string s consisting of the characters 'a', 'b', and 'c' and a non-negative integer k. Each minute, you may take either the leftmost character of s, or the rightmost character of s.
Return the minimum number of minutes needed for you to take at least k of each character, or return -1 if it is not possible to take
k of each character.
Example 1:
Input: s = "aabaaaacaabc", k = 2Output: 8
Explanation:
Take three characters from the left of s. You now have two 'a' characters, and one 'b' character.
Take five characters from the right of s. You now have four 'a' characters, two 'b' characters, and two 'c' characters.
A total of 3 + 5 = 8 minutes is needed.
It can be proven that 8 is the minimum number of minutes needed.
Example 2:
Input: s = "a", k = 1Output: -1
Explanation: It is not possible to take one 'b' or 'c' so return -1.
Constraints:
1 <= s.length <= 105sconsists of only the letters'a','b', and'c'.0 <= k <= s.length
You are given two integers m and n representing a 0-indexed m x n grid. You are also given two 2D integer arrays guards and walls where guards[i] = [rowi, coli] and walls[j] = [rowj, colj] represent the positions of the ith guard and jth wall respectively.
A guard can see every cell in the four cardinal directions (north, east, south, or west) starting from their position unless obstructed by a wall or another guard. A cell is guarded if there is at least one guard that can see it.
Return the number of unoccupied cells that are not guarded.
Example 1:
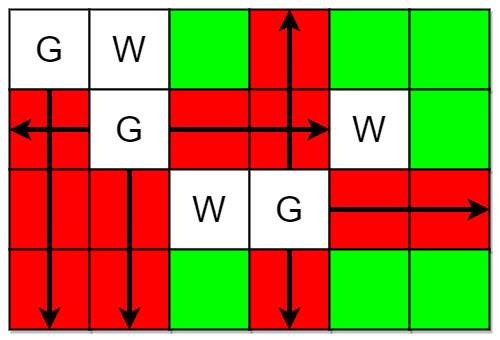
Input: m = 4, n = 6, guards = [[0,0],[1,1],[2,3]], walls = [[0,1],[2,2],[1,4]]
Output: 7
Explanation: The guarded and unguarded cells are shown in red and green respectively in the above diagram.
There are a total of 7 unguarded cells, so we return 7.
Example 2:
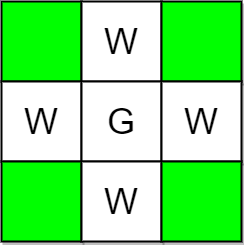
Input: m = 3, n = 3, guards = [[1,1]], walls = [[0,1],[1,0],[2,1],[1,2]]
Output: 4
Explanation: The unguarded cells are shown in green in the above diagram.
There are a total of 4 unguarded cells, so we return 4.
Constraints:
1 <= m, n <= 1052 <= m * n <= 1051 <= guards.length, walls.length <= 5 * 1042 <= guards.length + walls.length <= m * nguards[i].length == walls[j].length == 20 <= rowi, rowj < m0 <= coli, colj < n- All the positions in
guardsandwallsare unique.